To Estimate the Width of the Hadley Circulation We Assumed the Potential Temperature Was Continuous

Lectures on Tropical Meteorology

Chapter 5. The Hadley circulation

The early work on the mean meridional circulation of the tropics was motivated by observations of the trade winds. Halley (1686) and Hadley (1735) concluded that the trade winds are part of a large-scale circulation which results from the latitudinal distribution of solar heating. This circulation, now known as the Hadley circulation, consists of upward motion at lower latitudes, poleward motion aloft, sinking motion at higher latitudes and low-level equatorial flow. Despite the absence of upper-air observations Hadley deduced that the upper-level flow has a westerly component due to the effect of the earth's rotation.

The mean zonally-averaged circulation of the atmosphere is illustrated in Fig. 1. The annual mean (Fig. 1c) shows two thermally-direct circulations, the Hadley Cells, with ascent at the equator and descent at 30^oN and 30^oS. The Hadley cells are broadly symmetric about the equator in the annual mean, although with a slight displacement into the northern hemisphere. In each hemisphere there is a subtropical westerly upper-level jet located just polewards of the descending branch of the Hadley cell. In the northern hemisphere winter (DJF) (Fig. 1a) the northern Hadley cell is much stronger and broader than the southern cell. The location of the ascending branch has moved south of the equator into the summer hemisphere. The westerly jet in the northern hemisphere is stronger and further south than in the annual mean.

Figure 1. The zonal mean zonal wind and vectors of the meridional wind for (a) December-January-February, (b) June-July-August, and (c) the annual mean, based on six years of ECMWF data. Contour interval 5 m s^-1, with values in excess of 20 m s^-1 shaded. The horizontal sample arrow indicates a meridional wind of 3 m s^-1, and the vertical sample arrow a vertical velocity of 0.03 Pa s^-1. (From James, 1994)

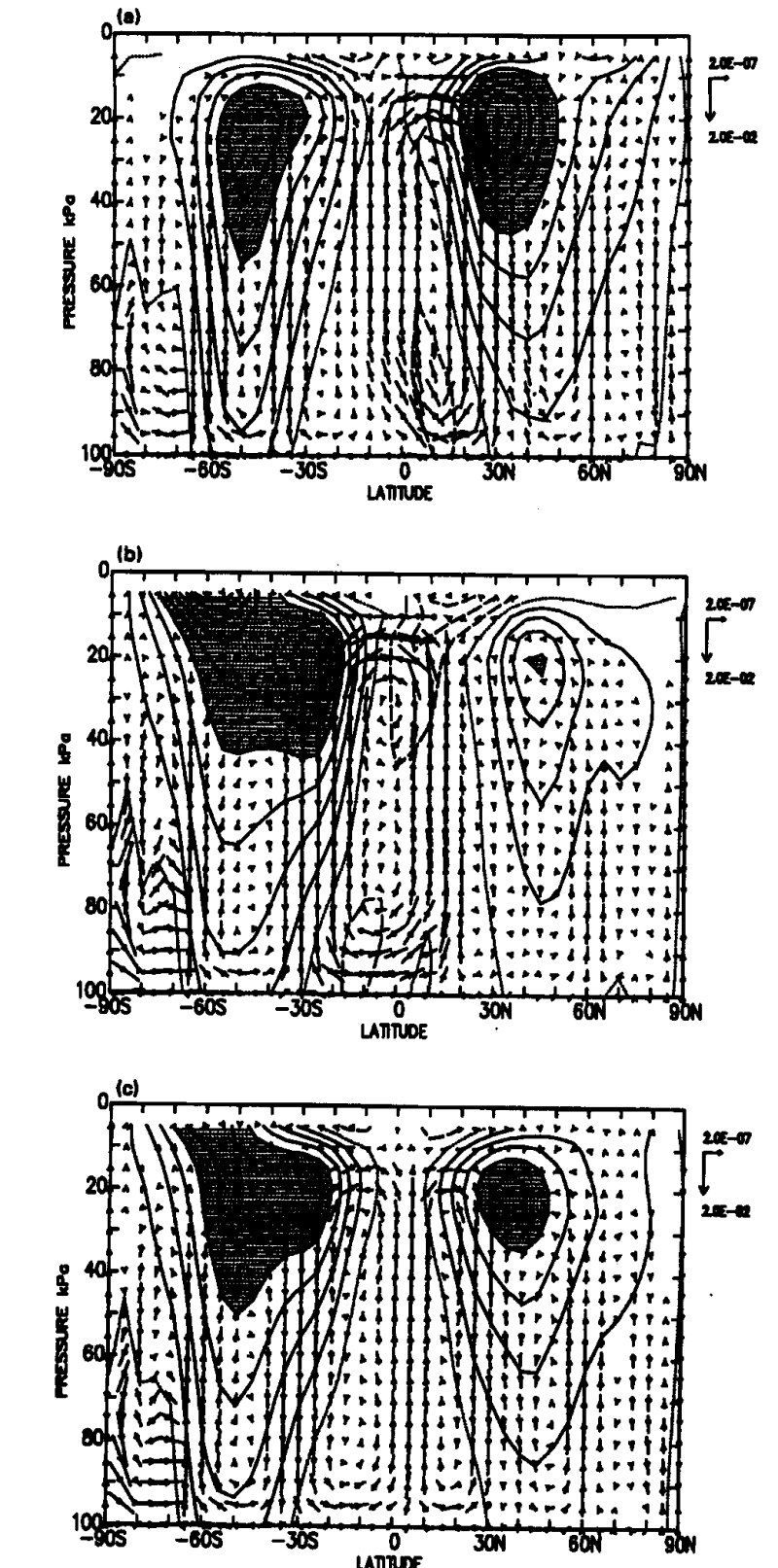In the southern hemisphere winter (Fig. 1b) the southern Hadley cell dominates the tropical circulation, the northern Hadley cell is weak and very narrow. The maximum ascent is north of the equator in the summer hemisphere and the southern hemisphere westerly jet shows a double jet structure with a maximum at the location of the descending branch of the Hadley cell and a second maximum further south.

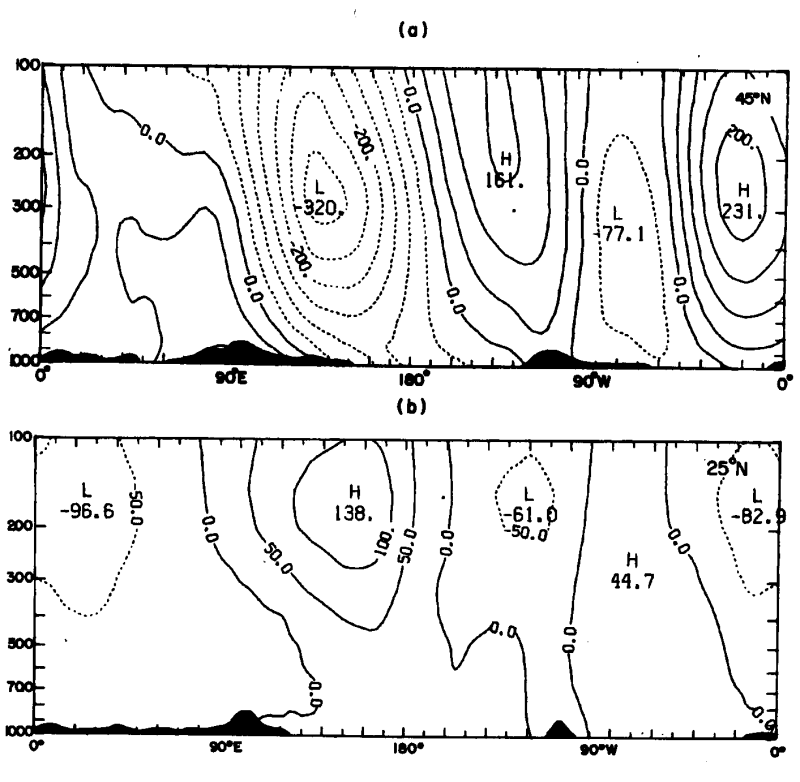
In the tropical troposphere the departure from zonal symmetry is much smaller than that in midlatitudes. This is illustrated in Fig. 2 which shows the departures from zonal symmetry of the time-averaged geopotential height. The cross-section at 45^oN shows substantial eddy activity (Substantial in the sense that fluctuations about the mean are comparatively large.) throughout the troposphere. In contrast, at 25^oN the eddy activity has much smaller amplitude in the troposphere. Thus we can use an axisymmetric model to develop a simple model of the Hadley circulation. Such a model was developed by Held and Hou (1980). The description of this model given here closely follows that of James (1994).

Figure 2. Longitude-height cross-sections of the departure from zonal symmetry of the time-averaged geopotential height taken along (a) 45^oN and (b) 25^oN. The contour interval is 50 m. The local orography is depicted at the bottom of the figures. (From Gill, 1982)

5.1 The Held-Hou Model of the Hadley Circulation

The Held-Hou model is symmetric about the equator and assumes steady, linear, axisymmetric flow in hydrostatic balance. The main features of the model are a simplified representation of solar heating and the use of angular momentum conservation and thermal wind balance. The model aims to predict the strength and the width of the Hadley circulation.

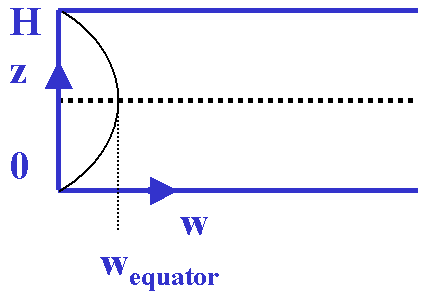
The Held-Hou model is a two-level model on the sphere with equatorward flow at the surface and poleward flow at height H, as illustrated in Fig. 3. The radius of the earth is a, the angular velocity of the earth Ω, and the latitude φ. The thermal structure is described by the mid-level potential temperature, θ.

Radiative processes are represented in the model using a Newtonian cooling formulation in which the potential temperature of the model is driven towards a prescribed radiative equilibrium potential temperature profile, θ_E, on a time scale τ_E. Mathematically, we write

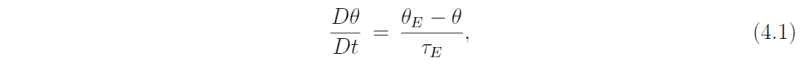
where

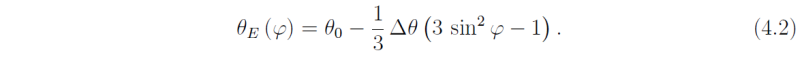
In the latter expression, θ₀ is the global mean radiative equilibrium temperature and Δθ is the equilibrium pole-to-equator temperature difference.

Figure 3. Schematic illustration of the Held-Hou model. (From James, 1994)

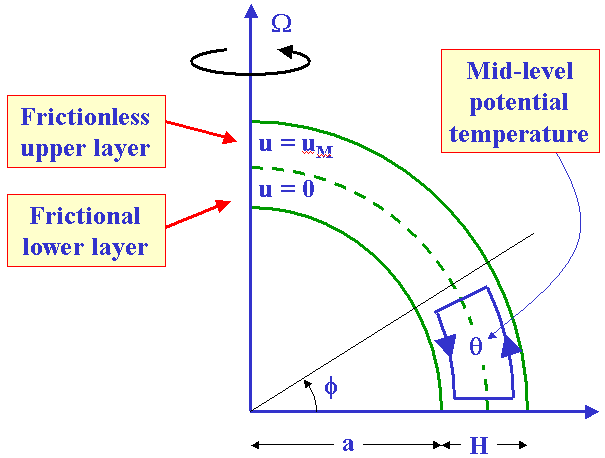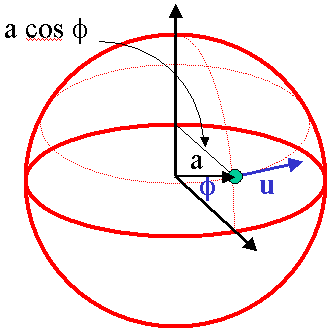
It is assumed that, as a result of friction at the ground, the zonal wind at the surface is much smaller than the zonal wind at height H and can be neglected. The zonal flow at height H, U_M, is calculated on the assumption of conservation of angular momentum as follows. Let u be the zonal velocity of a ring of air at latitude φ. Then the specific2 absolute angular momentum of the ring is given by (Ωa cos φ + u)a cos φ, where a is the radius of the earth (see Fig. 4).

If we assume that u = 0 at the equator, the zonal flow at latitude φ is given by

Figure 4. Illustrating the absolute angular momentum of a parcel in spherical coordinates. The relative angular momentum is ua cos � and the angular momentum associated with the Earth�s rotation is (Ωa cos φ)².

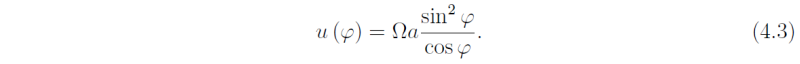
We simplify the algebra by assuming that φ is small (i.e. φ ≈ sin φ ≈ y/a). Then (4.2) becomes

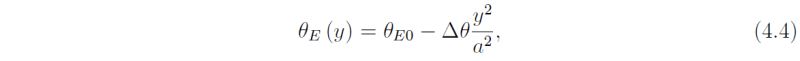
with θ_E0 = θ₀ + Δθ/3 and from (4.3), the upper-level zonal wind is

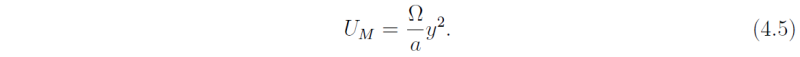
The rectangular configuration of the model is sketched in Fig. 5. The potential temperature structure at the middle level of the model is calculated from thermal wind balance. The approximation used is that f(∂u/∂z) = -(g/θ₀)(∂θ/∂y), where θ is the potential temperature, θ₀ is some reference potential temperature, f = 2Ωsinφ ≈ 2Ωy/a, and g is the acceleration due to gravity.

Figure 5. Rectangular configuration of the Held-Hou model.

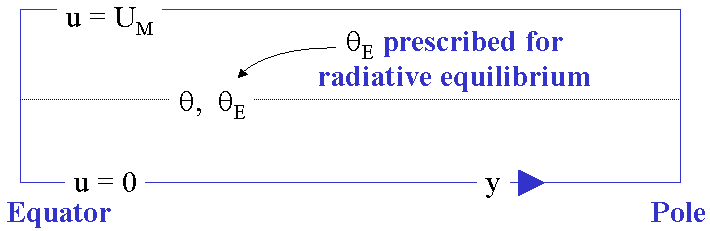With the assumptions of steady, linear, axisymmetric flow in hydrostatic balance, the thermal wind relation is satisfied even at low latitudes. As we have assumed that the zonal flow at the surface is much smaller than that at upper levels, the vertical shear in the zonal direction is

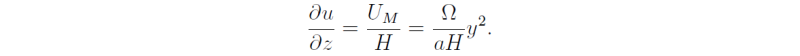
Then thermal wind balance gives the meridional potential temperature gradient

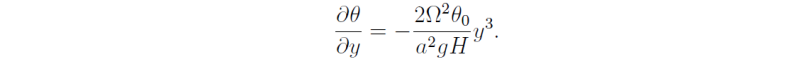
We can integrate this expression to obtain the potential temperature field

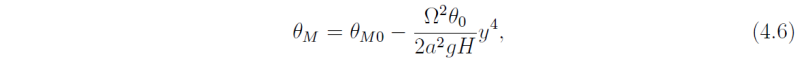
where the constant of integration, θ_M0, is the temperature at the equator. The subscript M is used here to remind us that the potential temperature field has been derived using conservation of angular momentum.

Figure 6 shows the equilibrium temperature, θ_E, and the model temperature, θ_M. The temperature curves intersect each other twice in each hemisphere, with θ_E > θ_M between the equator and the first crossing point, and θ_E < θ_M between the first and second crossing points.

Figure 6. Showing θ_E and θ_M as a function of poleward distance for the Held and Hou model. The constant θ_M0 must be chosen so that the areas between the two curves are equal, i.e. so that there is no net heating of air parcels. (Adapted from James, 1994).

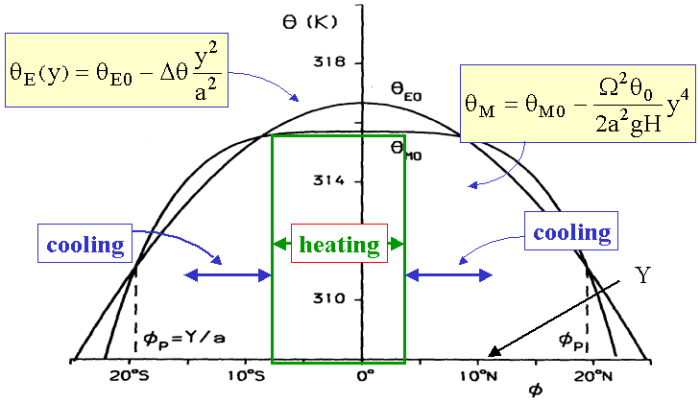From (4.1) we see that there is heating between the equator and the first crossing point, and cooling between the equator and the second crossing point. Heating occurs at latitudes higher than the second crossing point. Since this is unphysical we assume that the second crossing point, y = Y , marks the poleward boundary of the Hadley circulation. For y > Y the temperature is given by the radiative equilibrium temperature, θ_E.

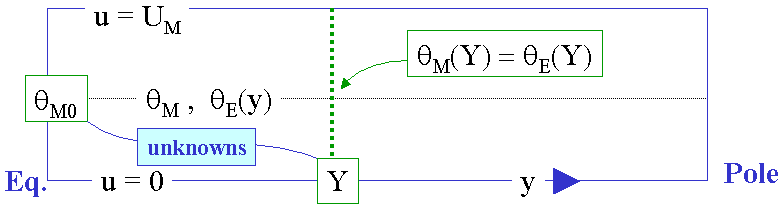
We have now two unknowns: the width of the Hadley cell, Y, and the equatorial temperature, θ_M0 (see Fig. 7). Since the model assumes a steady state, there can be no net heating of an air parcel when it completes a circuit of the Hadley cell, i.e.

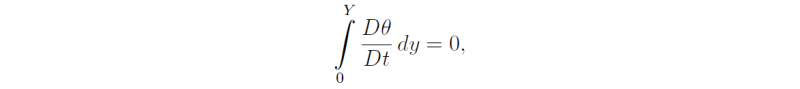
and from (4.1), assuming that τ_E is a constant,

Figure 7. The unknowns in the Held-Hou problem and the constraint at y = Y.

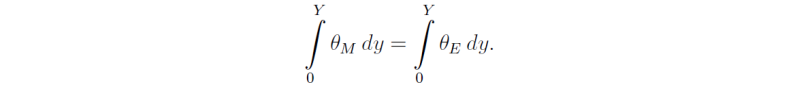
Using (4.4) and (4.6) we obtain

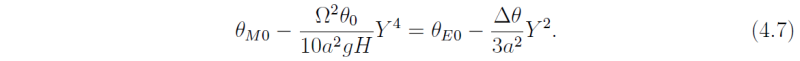
We assume continuity of potential temperature at y = Y so that θ_M(Y) = θ_E(Y). This gives

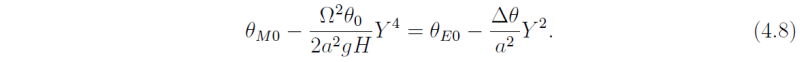
From (4.7) and (4.8) we obtain the width of the Hadley cell

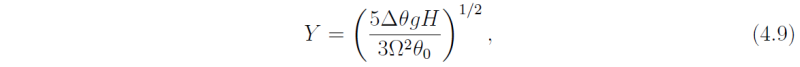
and the equatorial temperature

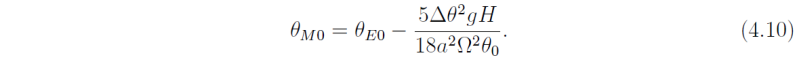
Taking θ₀ = 255 K, Δθ = 40 K, and H = 12 km gives the width of the Hadley cell to be approximately 2400 km and the equatorial temperature to be about 0.9 K cooler than the equilibrium equatorial temperature. The width of the Hadley cell from the simple model is roughly in agreement with observations (see Fig. 1), although it is somewhat too small.

Figure 8. Zonal wind structure, U(y), in the solution of the Held-Hou model.

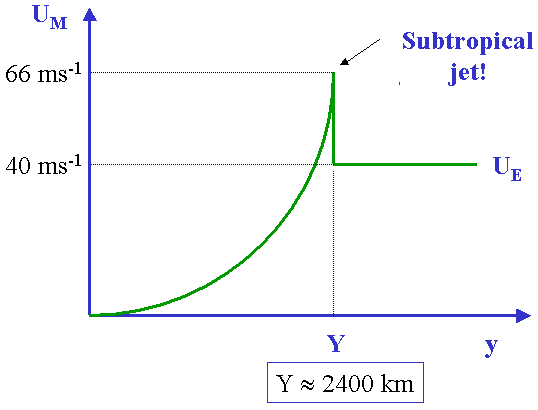The meridional variation of the zonal wind is given by (4.5) for y <= Y (see Fig. 4.8). The zonal wind increases quadratically with y to reach a maximum value of approximately 66 m s^-1 at y = Y . At higher latitudes the zonal wind can be calculated from thermal wind balance using the equilibrium temperature θ_E given by (4.4). This gives the zonal wind for y >= Y:

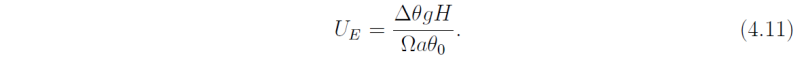
For the parameter values given above U_E is 40 m s^-1. Thus we see that there is a discontinuity in the zonal wind at the poleward boundary of the Hadley circulation. Although this discontinuity is not physical we could think of it as representing the upper-level jet observed in nature. Such a sharp jet would not be observed either in nature or in a more sophisticated model since it would be very unstable. The strength of the Hadley circulation in the Held-Hou model can be estimated as follows. By symmetry, v = 0 at the equator and (4.1) can be expressed as

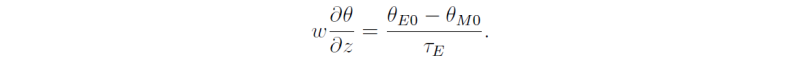
Assuming constant Brunt-Väisälä frequency, N, the middle-troposphere vertical velocity at the equator, w_H/2 is given by

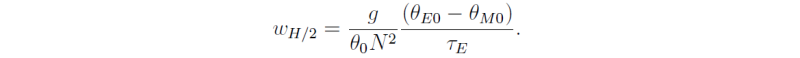
Using τ_E ≈ 15 days and N ≈ 10^-2 s^-1 gives w_H/2 ≈ 0.27 mm s^-1. Assuming that the vertical velocity varies quadratically with height, i.e., w = 4w_H/2z(H - z)/H², then (∂w/∂z)_z=H = -4w_H/2/H (see Fig. 9).

Figure 9. Assumed vertical variation of w across the domain.

From continuity, v_z=H ≈ 4Yw_H/2/H ≈ 21.6 m s^-1. Observations show that the strength of the meridional flow in the Hadley circulation is approximately 1 m s^-1. Thus although the Held-Hou model provides a reasonable estimate of the geometry of the Hadley circulation it gives a poor estimate of the strength of the circulation. Part of the reason may be the use of the Boussinesq approximation.

The Held-Hou model predicts that the width of the Hadley cell is inversely proportional to the planetary rotation rate (see (4.9)). This prediction has been confirmed in more realistic models of planetary atmospheres. At low rotation rates the Hadley cells extend far polewards and account for most of the heat transport from equator to pole. At high rotation rates the Hadley cells are confined near the equator and baroclinic waves polewards of the Hadley circulations re responsible for a significant proportion of the heat transport. For more details see, for example, James (1994, Ch. 10).

5.2 Extensions to the Held-Hou model

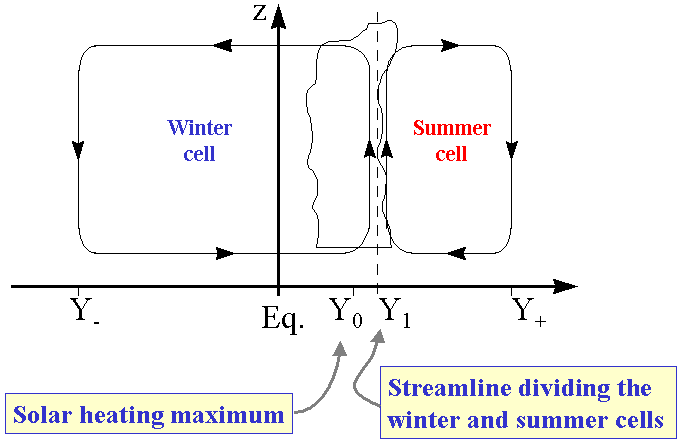
Although the Held-Hou model gives a reasonable estimate for the size of the Hadley circulation it gives a very poor estimate of its strength. A better model can be formulated by relaxing one of the assumptions of the Held-Hou model, namely that of symmetry about the equator. Although the annual mean solar heating is symmetric about the equator, the heating at any given time is generally not and thus the response to the solar forcing is not necessarily symmetric about the equator. Figure 1 shows that although the annual mean Hadley circulation is symmetric about the equator, the monthly mean Hadley circulation may be very asymmetric. Lindzen and Hou (1988) extended the Held-Hou model to allow for such an asymmetry whilst retaining the other assumptions described above.

The extended model is sketched in Fig. (4.10). The removal of the symmetry constraint means that the locations of maximum heating, maximum ascent, and the streamline dividing the summer and winter Hadley cells need not coincide. The solar heating is maximum at y = Y₀. The streamline dividing the summer and winter cells is located at y = Y₁ and the poleward extent of the summer and winter cells are given by Y₊ and YY_- respectively.

Figure 10. Schematic illustration of the Held-Hou model without the assumption of symmetry about the equator. Y₀ denotes the latitude of maximum heating, Y₁ the dividing streamline between the summer and winter cells. Y₊ and Y_- give the poleward extent of the summer and winter cells respectively.

Radiative processes are represented by (4.1) as before, but the equilibrium potential temperature is given by

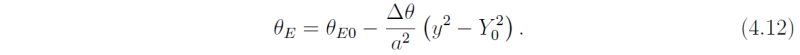
so that θ_E is maximum at Y₀. Conservation of angular momentum is used as before to calculate the upper-level zonal flow, with the assumption that the zonal wind is zero at the dividing streamline between the winter and summer cells, i.e. at y = Y₁. The upper-level zonal flow for small y is

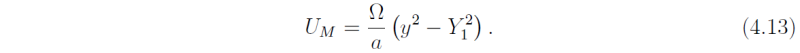
Using thermal wind balance we obtain the potential temperature

Figure 11. The Held-Hou model for asymmetric heating with maximum value at 6^oN. Here φ_W, φ₀, φ_c and φ_S correspond with y = Y_-, Y₀, Y₁ and Y₊ in Fig. (4.10). (From James, 1994)

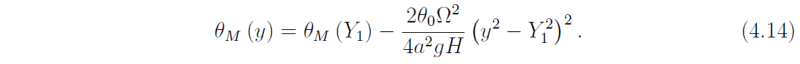
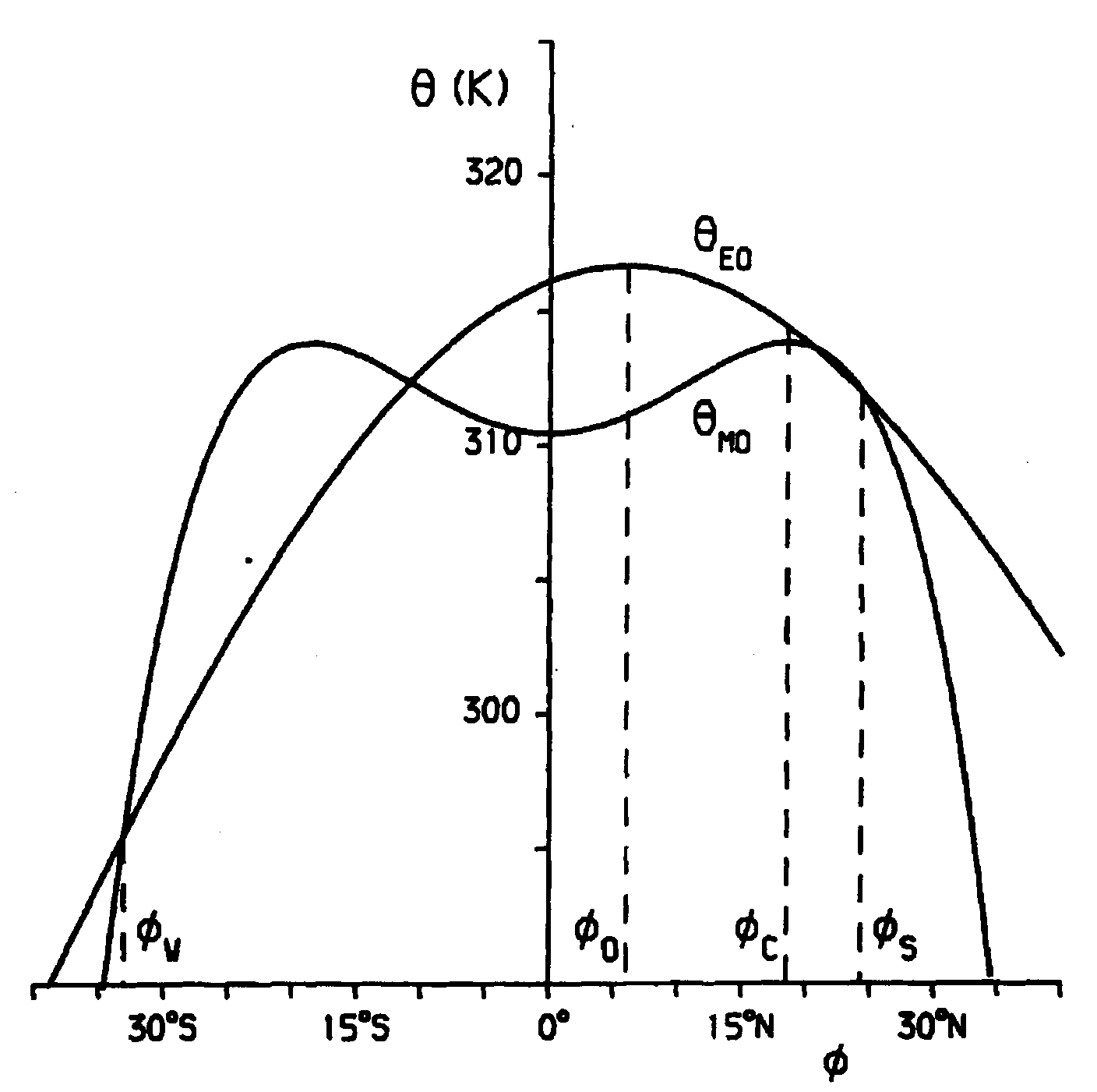Note that both U_M and θ_M are asymmetric about the equator. The asymmetry in the solution arises from the different size of the summer and winter cells. For |y| < |Y₁|, Eq. (4.13) gives U_M < 0, i.e. there are upper-level easterlies at the equator. The form of θ_E and θ_M is shown in Fig. (4.11). The poleward extent of each Hadley cell is defined as the second crossing point of the two potential temperature curves to the north or south of the latitude of maximum heating. Note that the magnitude of heating and cooling in the summer cell is much smaller than that in the winter cell. Figure (4.11) shows a strong asymmetry in the size of the summer and winter cells when the maximum heating is at 6^oN.

We have now four unknowns: Y₁, Y₊, Y_-, and θ_M(Y₁). These can be found using the conditions of no net heating for an air parcel completing a circuit of each cell:

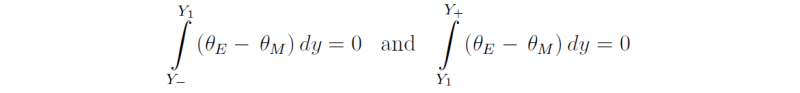
and of continuity of potential temperature at y = Y₊ and y = Y_-.

Figure 12. Results of the Held-Hou model for asymmetric heating with varying latitude of maximum heating. (a) Variation of the poleward extent of the summer and winter circulations and of the latitude of the dividing streamline. (b) Variation of the mass flux carried by the winter and summer cells. Here φ_W, φ₀, φ_c and φ_S correspond with Y_-, Y₀, Y₁ and Y₊ in Fig. (4.10). (From James, 1994)

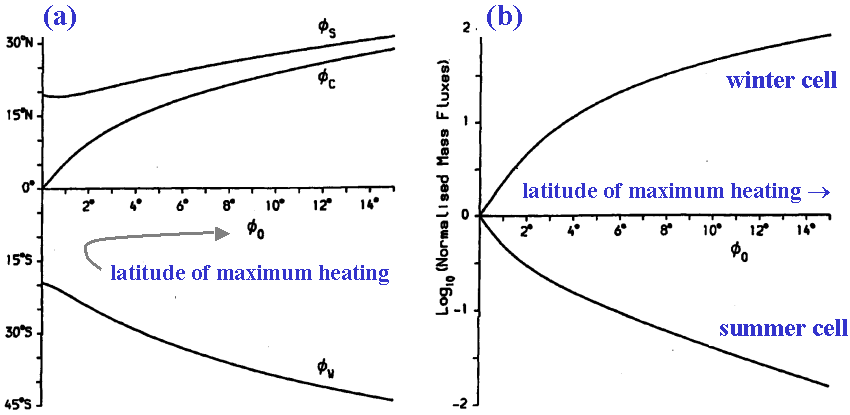The poleward extent of the two cells and the latitude of the dividing streamline are shown in Fig. (4.12a) for varying latitude of maximum heating. As the latitude of maximum heating increases the width of the summer cell decreases significantly. For maximum heating only 2^o away from the equator, the winter cell is over three times as wide as the summer cell. The relative width of the winter and summer cell changes most significantly for small displacements away from the equator of the latitude of maximum heating. The dividing streamline is always polewards of the latitude of maximum heating.

The mass flux in the winter and summer cells is shown in Fig. (4.12b), normalized by the mass flux for symmetric h eating. As the latitude of maximum heating moves away from the equator the mass flux carried by the winter cell increases strongly and that carried by the summer cell decreases. For maximum heating 4. away from the equator the mass flux in the winter cell is over an order of magnitude larger than that in the summer cell. When the maximum heating is 6. from the equator the difference in the mass fluxes is two orders of magnitude.

Figure 4.12 shows that both the strength and the width of the Hadley circulations are related to the latitude of maximum heating in a highly nonlinear manner. The Hadley circulation in the symmetric Held-Hou model is too weak because the annually averaged response to solar heating is much stronger than the response to the annually averaged heating. Discrepancies exist still between the results of this simple model and the observations. For example, the upper-level equatorial easterlies are too strong. However, it is perhaps more surprising that the model can reproduce many of the observed features of the zonally symmetric circulation, when one considers the nature of the approximations made.

Further improvements to the Held-Hou model can be made by including the effects of friction in the upper atmosphere and of moisture. Inclusion of these effects in the axisymmetric framework is discussed in James (1994 Section 4.3).

A more serious drawback of such simple models of large-scale overturning is that they are not consistent with the observed vertical profile of equivalent potential temperature, as discussed by Holton (1992, Ch. 11). The simple model requires air from the lower troposphere to rise uniformly and then move polewards, transporting heat from equator to pole. The vertical profile of equivalent potential temperature, θ_e, in the tropics (Fig. 4.13) exhibits a mid-tropospheric minimum. Large-scale ascent in this environment would lead to an increase in θ_e in the lower troposphere and a decrease in the upper troposphere, in other words, the observed distribution of θ_e could not be maintained.

Figure 13. Typical sounding in the tropical atmosphere showing the vertical profiles of potential temperature θ, equivalent potential temperature θ_e, and the saturated equivalent potential temperature θ_e ^*. (From Holton (1992), after Ooyama, 1969)

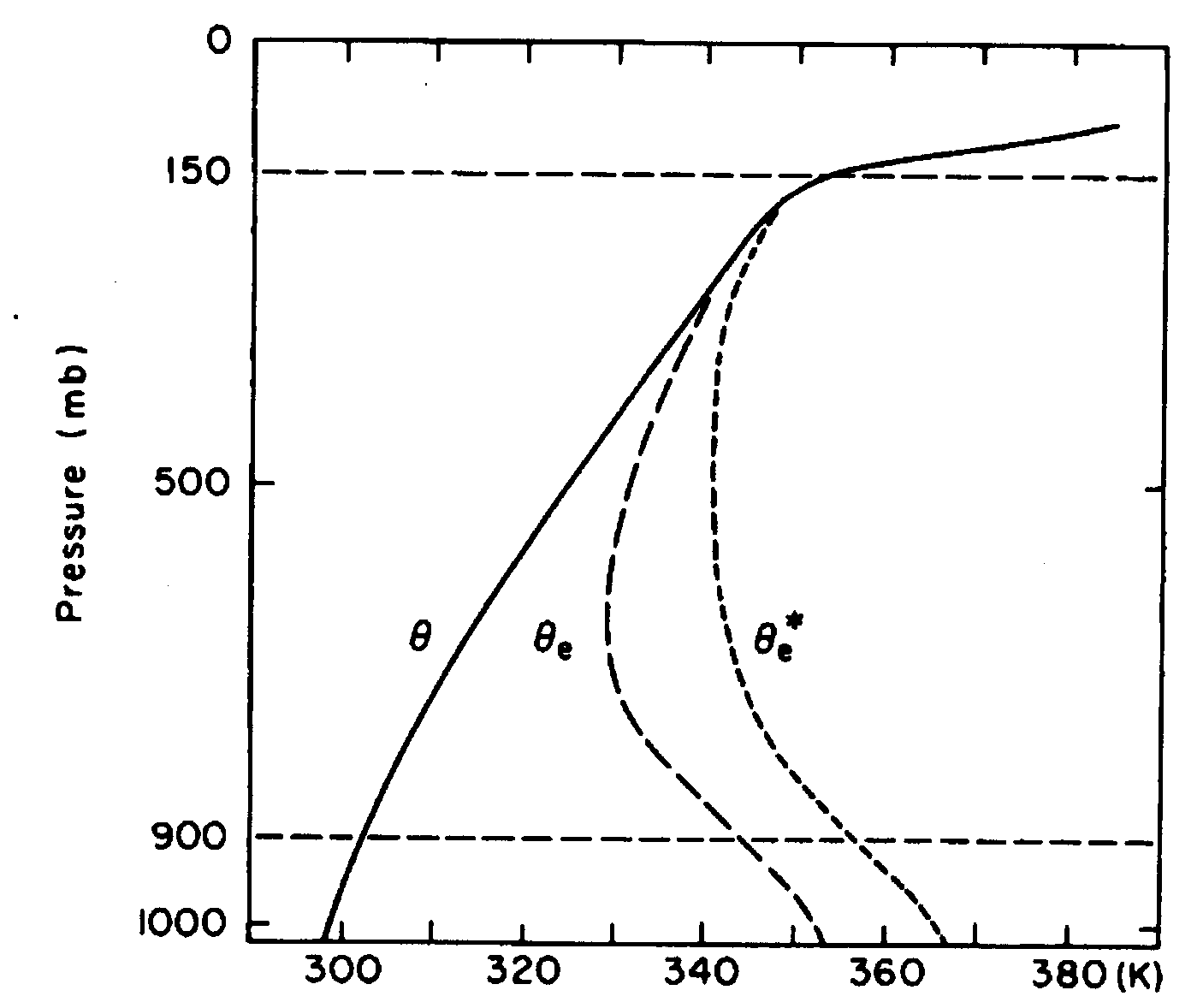In reality the ascending motion of the Hadley circulation takes place in deep convection in the ITCZ. Air parcels from the boundary layer which ascend in cumulonimbus towers through the environment shown in Fig. (4.13) can arrive at the tropopause with positive buoyancy. Riehl and Malkus (1958) estimated that of the order of 1500 - 5000 cumulonimbus towers are required simultaneously around the ITCZ to account for the required vertical heat transport.

5.3 Further reading on the Hadley Circulation

Lorenz, E. N., 1967: Extract from "The nature and theory of the general circulation of the atmosphere". (click here)

Lindzen, R. S. and A. Y. Hou, 1988: Hadley circulation for zonally-averaged heating centered off the equator. J. Atmos. Sci., 45, 2416-2427. (click here)

Hack, J. J., W. H. Schubert, D. E. Stevens, and H.-C. Kuo, 1989: Response of the Hadley circulation to convective forcing in the ITCZ. J. Atmos. Sci., 46, 2957-2973. (click here)

Satoh, M., 1994: Hadley circulations in radiative-convetive equilibrium in an axially symmetric atmosphere. J. Atmos. Sci., 51, 1947-1968. (click here)

Polvani, L. M. and A. H. Sobel, 2002: The Hadley circulation and the weak temperature gradient approximation. J. Atmos. Sci., 59, 1744-1752. (click here)

5.4 Other references

(click here)

---

Copyright © Roger Smith, Date 11 Jun 2015

hestonfamess.blogspot.com

Source: https://www.meteo.physik.uni-muenchen.de/~roger/Lectures/TropicalMetweb/TropicalMeteorology_Ch5.html

Share this post